Usability study of wearable inertial sensors for exergames (WISE) for movement assessment and exercise
Introduction
Recent years have witnessed the emergence of digital health using advanced technologies such as wearable sensors and embedded controllers to enhance access to medical diagnostics and treatments (1,2). Because of an accelerating trend in the number of stroke survivors requiring rehabilitation (3), healthcare services worldwide are considering technological solutions to enhance accessibility to assessment and treatment. For example, virtual therapists and telerehabilitation have been proposed to complement the skills of therapists (4,5). However, some of the challenges faced by these technologies are clinical acceptance, high equipment cost, accuracy, and ease of use (4).
Most tasks constituting activities of daily living have minimum range of motion (ROM) requirements at various joints (6). Restoring the ability to perform activities of daily living in individuals with impaired movement therefore requires clinicians to assess ROM and customize the exercises to each patients’ activity limitations. Commercially available devices such as goniometers (7), inclinometers (8), and videographic methods (9) are used by therapists to assess patient’s ROM in one-on-one clinical settings. Goniometers and inclinometers have limited inter-observer agreement due to variability in positioning the sensors on the patient’s body and can capture motion only for one joint at a time. Videographic methods also show low inter-observer agreement due to differences in camera positions and often require extensive post-acquisition data analysis. Furthermore, these methods are not suitable for remote assessments and individualized treatments, which are essential to enhance accessibility.
The Kinect™ V2 (Microsoft Corp., Redmond, WA, USA) is a popular markerless motion capture system used for gaming (10). The Kinect can provide high definition video output, depth information, and position information for 25 joints of the human body in 3D space (10). Several studies have reported the use of the Kinect sensor in ROM assessment and rehabilitative applications (11-19). Gait analysis and joint angle (JA) orientation measurements using the Kinect has shown varying levels of agreement for different joint segments (11,16,17,19,20). Under ideal conditions, the shoulder and elbow joint ROM measurements from the Kinect show good inter-trial repeatability and correlate with measurements taken with a goniometer (19,21). However, the placement of Kinect is a limiting factor: placing it in front of a subject yields reliable measurements in contrast to placing it on the side (22), but fails to correctly measure elbow flexion-extension accurately from a neutral position (11,22) and cannot measure forearm pronation-supination. Furthermore, a recent literature review on the use of repurposed gaming consoles, such as the Kinect, for neurorehabilitation in target populations reported an inability to provide individualized training as a major limitation (23).
An alternative approach for ROM and rehabilitation assessment applications is to use inertial sensors, which include inertial measurement units (IMU) and magnetic, angular rate, and gravity (MARG) sensors that measure the linear acceleration and angular velocity of a rigid body to which they are attached. Commercially available wearable inertial sensors for motion capture can be used for ROM assessment (24,25), but their use for rehabilitation is limited by the cost of custom data acquisition software, need for user-training, and the extensive data analysis required post-acquisition. Although (26,27) have shown that it is possible to extract absolute orientation of a rigid body from raw measurements of the IMU and MARG sensors, their methods are yet to be extended for use in rehabilitation applications requiring JA measurements.
Telerehabilitation is a branch of emerging medical innovation that permits assessment and treatment of patients remotely. Repurposed off-the-shelf media platforms (e.g., Skype, VSee, etc.) and interactive gaming consoles (e.g., Kinect, PlayStation, Wii, etc.) have been used in prior research efforts for telerehabilitation (28,29). However, most telerehabilitation applications are limited by (I) an inability to capture measurements accurately and with high inter-observer agreement easily in a remote manner and (II) provide individualized coaching asynchronously, i.e., without a live coach. To address these limitations, we designed a wearable inertial sensors for exergames (WISE) system consisting of: (I) an animated virtual coach to deliver virtual instruction for any activity and (II) a subject-model whose movements are animated by real-time sensor measurements using inertial sensors worn by a subject. In this paper, we test the WISE system’s accuracy and usability for assessment of upper limb ROM.
Methods
Design of WISE system
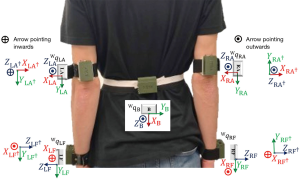
The WISE system consists of five wearable sensor modules affixed to the upper limb segments (Figure 1A). The sensors are labeled to correspond to placement on appropriate limb segments, i.e., sensors marked LF (i.e., left forearm) and RF (i.e., right forearm) are placed above the wrist on the left and right forearms, respectively; sensors marked LA (i.e., left arm) and RA (i.e., right arm) are placed above the elbow on the left and right arms, respectively; and the sensor marked B is placed on the back. Each WISE sensor module (30) consists of a BNO055 MARG sensor interfaced with a Gazell-protocol endowed microcontroller (µC) soldered to a printed circuit board (PCB). The PCB is connected to a lithium-ion battery housed in a 3D-printed wearable enclosure. The µC retrieves absolute orientation measurement from the MARG sensor and wirelessly streams it to a computer. A Unity3D-based exergame interface was developed to use the sensor data for animating a 3D-human model, i.e., the subject-model. The salient features of the application include (I) a sensor calibration user-interface (UI) (Figure 1B), (II) a sensor mounting UI (Figure 1C), (III) a virtual exercise environment (Figure 1D), and (IV) an instructor-programming UI (Figure 1E). Each BNO055 MARG sensor consists of in-built three-axes magnetometer, accelerometer, and gyroscope. The BNO055 sensor requires an initial calibration for streaming absolute orientation (31). A storage and calibration cube was designed and 3D-printed to house the five WISE system modules and simultaneously calibrate all the sensors prior to placement on a subject (Figure 1F). Sensor calibration UI allows intuitive visualization of each WISE module’s calibration status. The sensor mounting UI is a virtual environment that utilizes the data streamed to provide instructions to the user in neutral pose for mounting the sensors on their body to obtain accurate ROM measurements (32). The virtual exercise environment consists of an instructor model performing ROM exercises that are to be performed by the subject. The upper extremity (UE) motion of the subject-model is animated by the real-time data from the WISE modules worn by the subject. The instructor-programming environment allows an instructor to use the WISE modules to record exercises or activities in a flexible manner and replay them as “instructed exercises” performed by the virtual coach (32). We used the instructor-programming environment to record a series of ROM exercises using the WISE system for the testing protocol of this paper.

ROM measurements for WISE (30)
Each WISE module streams quaternion data of its orientation relative to the world coordinate frame (ℱW), which is represented by the direction of earth’s gravity and the magnetic north pole. Quaternions are four-tuple objects that provide a computationally effective way to represent orientation (33). A quaternion q = (qw qx qy qz) consists of a scalar part qw and a vector part [qx qy qz]T. Three dimensional vectors are a subset of quaternions and a quaternion with its scalar part qw =0 is termed a vector quaternion. Other forms of orientation representation include Euler angles, axis/angle representation, and rotation matrices (33). Consider the axis/angle representation (d, φ) where d = [dx dy dz]T is the axis of rotation and φ is the angle of rotation, then the corresponding quaternion describing this rotation is given below.
[1]
A vector
[2]
where “⊗” and “*” denote the quaternion product (27,34) and conjugate,
Although quaternions provide an efficient tool for orientation computation, they are unintuitive for interpretation by rehabilitation practitioners. In contrast, Euler angles represent rotations of one coordinate frame relative to another characterized by simple rotations about their principal axes. The joint coordinate system (JCS) framework, proposed by the International Society of Biomechanics, recommends the use of Euler angles for extracting anatomical JAs for ease of use by practitioners (35). The UE JA measurements discussed in (35) utilize the proximal coordinate frame as a reference to describe the angular rotation of the distal coordinate frame, i.e., the shoulder and elbow JA computations use the back and arm WISE modules, respectively, as references. To produce a reference for the shoulder JA computation, the back WISE module’s quaternion is rotated and stored as qLBref and qRBref as below:
[3]
The sign convention for shoulder JA measurement is as follows: extension (−), flexion (+), adduction (−), abduction (+), external rotation (−), and internal rotation (+). To follow a similar sign convention, the axes of qLA, qRA, qLBref, and qRBref are flipped [see Figure 2 where (·)† denotes the quaternions for the flipped coordinate frames]. This axis flipping operation is performed by converting the quaternions to rotation matrices (33), followed by multiplication of −1 to the row vectors corresponding to the coordinate axes that are to be flipped. Throughout the axes flipping operation, care is taken to ensure that the rotations follow the right-hand rule. The relative quaternions between the shoulder and back’s reference coordinate frame are computed as below.
[4]
[5]
To obtain the JA of the left and right shoulders, Wu et al. (35) suggest the use of the Y − X − Y' Euler angle convention. Since the five WISE modules were assigned sensor coordinate frames consistently (Figure 2), the appropriate placement and orientation of the LA and RA modules on arms required a slight adaptation of the framework of (35), leading to the use of Y − Z − Y' Euler angle convention (33) to obtain the JA of the left and right shoulders using the relative quaternions qLS and qRS. The quaternion to Euler angle conversion in the Y – Z − Y' framework produces angles θY, θZ, and θY + θY' that represent the shoulder plane, shoulder elevation, and shoulder internal-external rotation angles, respectively. In the JCS framework, the shoulder elevation angle θZ relates to shoulder flexion-extension when θY ≈90° and to shoulder abduction-adduction when θY ≈0° (35).
The elbow JA computation utilizes the JCS framework to compute the ROM for flexion-extension and pronation-supination with the WISE system. Identical to the procedure of shoulder JCS ROM computation, qLA and qRA are used to create references qLAref and qRAref as below:
[6]
[7]
To conserve the standard sign convention of elbow joint movements flexion (+), pronation (+), extension (−), and supination (−), the coordinate axes of qLAref, qRAref, qLF, and qRF are flipped similar to the procedure for shoulders. The relative quaternions between the elbow and shoulder’s reference coordinate frame are computed as below:
[8]
[9]
To obtain the elbow JA, Wu et al. (35) suggest the use of the Z − X − Y Euler angle convention. Thus, using the relative quaternions qLE and qRE with the quaternion to Euler angle conversion in the Z − X − Y framework produces elbow JA θZ, θX, and θY that correspond to the flexion-extension, carrying, and pronation-supination angles, respectively. The carrying angle is the angle between the humerus and the ulna, which is constant depending on the gender of the person ranging between 8° to 20° (36,37). For further details on the mechanics of ROM measurements for WISE see (30).
ROM measurements for Kinect
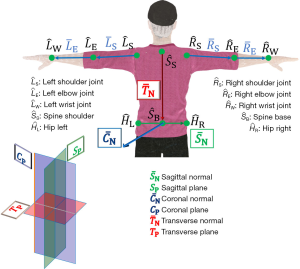
The Kinect provides a total of 25 joint coordinates of a human in 3D workspace extracted from the image and depth information (10). However, measurements from the Kinect do not yield sufficient information to characterize movement in the JCS framework. Specifically, by using the shoulder, elbow, and wrist positions obtained from the Kinect, it is not possible to resolve the three principal axes (35) corresponding to each of the shoulder and elbow joints. Thus, instead of using the JCS framework for computing shoulder abduction-adduction and flexion-extension, we adapt the vector projection approach of (19).
To illustrate the JA computation from the Kinect, we use characters with bar accent to denote vectors, e.g., “
[10]
The shoulder JAs are defined as follows: (I) shoulder flexion-extension (θFE) is the movement of the arm vector
[11]
[12]
The forearm vectors are constructed from the joint coordinates of elbows and wrists, similar to Eq. [10]. The left elbow flexion-extension αLFE angle computation is performed as below.
[13]
Note that the forearm pronation-supination angle cannot be computed from the Kinect data due to the lack of sufficient information.
The shoulder internal-external rotation (θIE) of the LA or RA cannot be computed with the information of shoulder vectors
[14]
Thus, the shoulder internal-external rotation calculation works only if the elbow is flexed beyond 30°. Finally, the computation for the right side of the body also utilizes similar equations as above and care is taken to ensure that extension, adduction, and external rotation are denoted as (−). Figure 3 illustrates all the UE joint coordinates and vectors used for the calculation of JA with the Kinect data.
Matching measurements from WISE and Kinect systems
As delineated above, unlike with the WISE system, measurements from the Kinect cannot use the JCS framework. Thus, the WISE system is modified to facilitate one-on-one comparison with the Kinect-based measurements of the computation of shoulder flexion-extension {Eq. [11]} and abduction-adduction {Eq. [12]}. The modified approach, adapted from (19), is outlined below.
The principal axes of the WISE module B
[15]
[16]
The angles for the right side are computed similar to Eq. [15] and Eq. [16] so that the signs of flexion and abduction are (+).
Subject recruitment and data collection
Seventeen healthy subjects (11 male and 6 female) were recruited for the study in the following age groups: 18–24 years (n=8), 25–34 years (n=6), 35–44 years (n=1), 45–54 years (n=1), and 55–64 years (n=1). The participants signed informed consent as approved by the NYU Institutional Review Board (IRB-FY2019-3426). Data collection took place at the Mechatronics, Controls, and Robotics Lab, NYU Tandon School of Engineering. The participants wore the WISE modules without any obstruction to their active ROM and stood at a distance of six feet in front of the Kinect with a white screen on their back to mitigate any changes to the ambient lighting. Video tutorials recorded with a 3D animated human model served as the virtual coach displayed on a television screen. The virtual coach demonstrated each exercise first and then instructed the subjects to perform the demonstrated exercises along with the coach for eight trials of the ten ROM exercises. At the end of the session, subjects were presented with a system usability scale (SUS) questionnaire that consisted of ten questions (with five positive and five negative statements). The questionnaire sought respondents’ opinion about using the virtual coach for ROM exercises on a five-point Likert scale.
Using MATLAB version 2019a (MathWorks, Inc., Natick, MA, USA), a routine was created for real-time data acquisition to compare the WISE and Kinect measurements. The experimental setup is illustrated in Figure 4. Three user interfaces were created: (I) a video display for subjects to view the virtual coach (Figure 4B); (II) Kinect’s video stream superimposed with numerical values of the JAs computed from the Kinect and WISE systems (Figure 4E); and (III) animated plots for JA visualization from the Kinect and WISE systems. Each subject performed the ROM exercises in the following sequence: (I) left shoulder flexion-extension (θLFE), (II) left shoulder abduction-adduction (θLBD), (III) left elbow flexion-extension from neutral-pose

Data processing and statistical analysis
The data was analyzed using MATLAB with the command findpeaks to determine the peak ROM measured using the Kinect
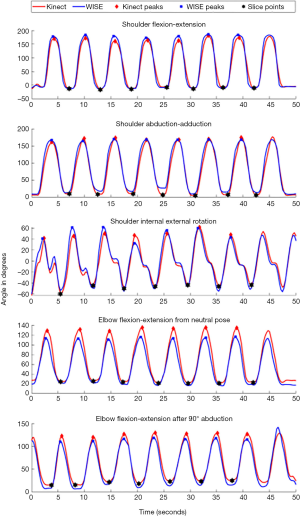
MATLAB environment’s data acquisition used a line-by-line program execution which caused a systematic lag/lead between the Kinect and WISE measurements. To mitigate the temporal error, we applied dynamic time warping (DTW) (38) to the Kinect and WISE measurements using the MATLAB command dtw similar to the procedure outlined in (14). Prior to applying DTW, the time series JA signals were scaled to [−1,1] by using the corresponding peak values for the Kinect and WISE measurements. Following the application of DTW, the data were rescaled by the peak values used previously for scaling. The peak and RMSE calculations described above were repeated using the JA output of DTW to compute the mean (μDTW) and standard deviation (σDTW) of the RMSE for each trial.
The Bland-Altman statistic establishes the agreement between two measurement systems by computing the limits of agreement (LOA) (39). Following the application of DTW, the error signal between the Kinect and WISE measurement systems exhibited high kurtosis and skewness indicating a non-normal distribution. Thus, Kimber’s outlier rejection technique (40) was applied to reject outlier data points beyond [Q1 − γ(M − Q1), Q3 + γ(Q3 − M)], where Q1, Q3, and M denote the first quartile, third quartile, and median, respectively. The multiplier γ =1.5 is a commonly used parameter for outlier rejection (40), thus it was used for rejecting the outliers in the Kinect and WISE measurements. The outputs of the outlier rejection procedure also exhibited non-normal distributions in the error signal. Thus, the Bland-Altman test for non-parametric signals, which defines the LOA as the median ±1.45 times the interquartile range (i.e., M ±1.45× IQR), was applied to the remainder of the Kinect and WISE data after the outlier rejection. The peaks obtained from the Kinect and WISE measurements after DTW were also used to compute the intra-class correlation coefficients (ICC). Two methods were used to determine (I) the test-retest consistency [ICC(C,1)] of the Kinect (ICCK) and WISE (ICCW) between trials and (II) the absolute agreement [ICC(A,1)] between the measurements of ROM peaks of the Kinect and WISE (ICCK/W) (41). The SUS responses for ten questions obtained from the subjects were analyzed for reliability using the Cronbach’s alpha (42,43) and the final SUS score was computed using the method described in (44).
Results
The mean and standard deviations of the RMSE between the JA measurements obtained from the Kinect and WISE systems for 17 subjects and 10 ROM exercises, Bland-Altman LOA, ICC for each device (ICCK, ICCW), and the absolute agreement between the two devices (ICCK/W) are shown in Table 1. The mean of the RMSE shows that the ROM measurements in the coronal, transverse, and sagittal planes had errors of less than 9°, 10°, and 12°, respectively. After the application of DTW, the mean RMSE errors in the coronal, transverse, and sagittal planes decreased to less than 8°, 8°, and 10°, respectively. The Bland-Altman LOA, with 95% confidence intervals, for ROM measurements in the coronal, transverse, and sagittal planes were determined to be in the range of (−12.0°, 10.0°), (−9.5°, 10°), and (−14.0°, 18.0°), respectively. The ICC for the Kinect (ICCK) and WISE (ICCW) systems indicated very good repeatability within each system especially for RA movements and slightly lower for left arm movements. The ICC was lowest for the left shoulder internal-external rotation. The ICCK/W, which compared the consistency between the Kinect and the WISE systems, showed moderate to very good agreement for all movements except the left and right elbow flexion-extension from the neutral-pose.
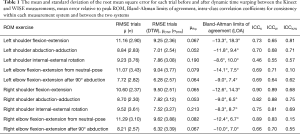
Full table
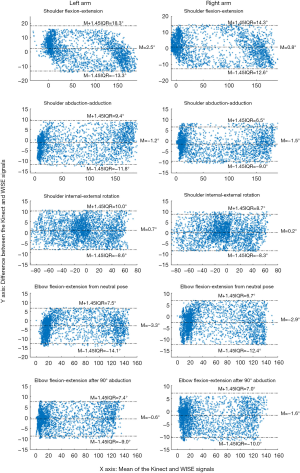
The Bland-Altman plots (i.e., mean versus difference) for the DTW-processed signals of the Kinect and WISE systems for the 10 ROM exercises are presented in Figure 6. The measurements for coronal plane ROM exercises (I) left and right elbow flexion-extension with 90° shoulder abduction and (II) right shoulder abduction-adduction produced Bland-Altman LOA within ±10°. However, for left shoulder abduction-adduction measurements the LOA was (−12.0°, 9.4°), which is slightly higher than the ±10° range. The transverse plane ROM exercises for the left and right shoulder internal-external rotation with 90° elbow flexion were also within the ±10° acceptance limits.
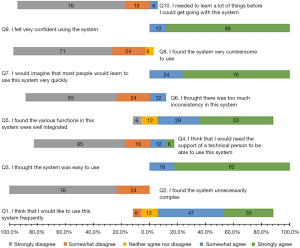
The SUS response percentages are plotted in a bar chart as shown in Figure 7. The Cronbach’s alpha for the five-point SUS scale for the ten questions was computed to be above 0.7, indicating acceptable reliability. A majority of the users found the virtual coach-based ROM tutoring system to be easy to use (82% strongly agreed) and well-integrated (82% agreed or strongly agreed) and reported that they would be confident in using it (88% strongly agreed) and would like to use it (82% agreed or strongly agreed). Overall, the SUS score showed relatively high third and first quartile scores of 97.5 and 82.5, respectively, with the interquartile range of 15 and the minimum score of 65, suggesting that the subjects were interested in using the animated virtual coach for the guided ROM exercises.
Discussion
Accurate assessment of ROM limitations and compliance monitoring of exercises to restore movement are necessary to assess and tailor treatments for individuals with motor deficits across care settings. In this paper, we presented the overview of the WISE system consisting of: (I) an animated virtual coach to deliver virtual instruction for any activity and (II) a subject-model whose movements are animated by the real-time sensor measurements using inertial sensors worn by a subject. We compared the accuracy and usability of the WISE system for assessment of upper limb ROM with the Kinect, which has been used extensively in prior studies as a markerless motion capture system for exergames and rehabilitation.
The results show moderate to very good within-device agreement for each of the measurement systems. The discrepancy between the two devices was within ±10° for most of the ROM exercises. The between-device agreement was moderate to very good in the coronal and transverse planes for the following ROM exercises: (I) shoulder abduction-adduction, (II) elbow flexion-extension with the shoulder abducted at 90°, and (III) shoulder internal-external rotation. Even though, there are no quantified clinical acceptance limits for the ROM assessment, prior literature (8) has suggested ±10° as acceptable LOA for the Bland-Altman statistic. Furthermore, the RMSE and Bland-Altman LOA results suggest the concurrence between the two measurement systems was best in the coronal plane. However, the RMSE for exercises in the sagittal plane, i.e., (I) elbow flexion-extension from neutral-pose and (II) shoulder flexion-extension showed greater discrepancy between the two devices. These discrepancies persisted despite the adaptation of the Kinect-based vector projection method (19) for computing JAs with the WISE system. This can be explained by the problem of joint occlusion during movements in the sagittal plane when the Kinect is placed in front of the subject (22). Alternatively, when the elbow flexion-extension exercise was performed with the shoulder abducted at 90°, the occlusion did not occur and resulted in the least discrepancy between the two systems. Next, the ROM exercises for internal-external rotation in the transverse plane were modified by the introduction of 90° elbow flexion, which enabled the use of elbow vector obtained from the Kinect measurements for the computation of shoulder internal-external rotation angle. Furthermore, the forearm pronation-supination angles could not be computed from the Kinect measurements. Although Kinect has been used extensively for exergames and rehabilitation, above results suggest that JA measurements from such markerless motion capture devices lack the ability to resolve motion in three planes of movement for each joint (i.e., shoulder and elbow) as required by the JCS framework. In contrast, the WISE system provides a robust integration of measurements from multiple wearable sensors for the shoulder and elbow joints allowing continuous real-time measurements of JAs in three planes for each joint. Finally, the SUS scores suggest that subjects were interested in using the animated virtual coach for the guided ROM exercises.
In a prior study, we developed a method to remotely assess grasping performance using real-time data (45) in patients with multiple sclerosis (46). Using the WISE system, a similar telerehabilitation intervention can be developed for patients in need of UE ROM assessment and rehabilitation exercises. In such a scenario, the therapists can use the virtual coach to provide an individualized battery of exercises, enabling patients to perform exercises at home while asynchronous measurements using the WISE platform can capture and transmit the information to the therapist. The granular ROM data in all three planes can be useful to bridge the gap between laboratory research on motion analysis and translation to clinical practice. Although the current implementation of the WISE system was restricted to a computer-based interface, in our prior work we have demonstrated the feasibility of interfacing medical devices with smartphones (47). In a similar vein, the WISE system can be interfaced to mobile devices such as tablets and smartphones to render a portable mHealth system. Future work will consider the use of the WISE virtual coach and a guided mounting interface for the sensors, as well as feedback systems that enable the virtual coach to tailor exercises based on the data acquired from the sensors.
Acknowledgments
The authors acknowledge the members of the Mechatronics, Controls, and Robotics Lab for assisting with subject recruitment and Mr. Hassam Khan Wazir for the selection of MARG sensors.
Funding: This work is supported in part by the National Science Foundation DRK-12 Grant DRL-1417769, RET Site Grant EEC-1542286, and ITEST Grant DRL-1614085; NY Space Grant Consortium Grant 48240-7887; and Translation of Rehabilitation Engineering Advances and Technology (TREAT) grant NIH P2CHD086841.
Footnote
Provenance and Peer Review: This article was commissioned by the Guest Editor (Mei R. Fu) for the series “Real-Time Detection and Management of Chronic Illnesses” published in mHealth. The article was sent for external peer review organized by the Guest Editor and the editorial office.
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/mhealth-19-199). The series “Real-Time Detection and Management of Chronic Illnesses” was commissioned by the editorial office without any funding or sponsorship. PR and VK have patented technology for a Game-Based Sensorimotor Rehabilitator through NYU. PR reports consulting for Mirrored Motion Works, Inc., outside the submitted work. The authors have no other conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The participants signed informed consent as approved by the NYU Institutional Review Board (IRB-FY2019-3426).
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Edwards J. Wireless sensors relay medical insight to patients and caregivers. IEEE Signal Processing Magazine 2012;29:8-12. [Crossref]
- Kim J, Campbell AS, de Ávila BE, et al. Wearable biosensors for healthcare monitoring. Nat Biotechnol 2019;37:389-406. [Crossref] [PubMed]
- Benjamin EJ, Muntner P, Alonso A, et al. Heart disease and stroke statistics—2019 update: A report from the American Heart Association. Circulation 2019;139:e56-528. [Crossref] [PubMed]
- Burdea GC. Virtual rehabilitation—Benefits and challenges. Methods Inf Med 2003;42:519-23. [Crossref] [PubMed]
- van Vuuren S, Cherney LR. A virtual therapist for speech and language therapy. In: Bickmore T, Marsella S, Sidner C. editors. Intelligent Virtual Agents. Springer, Cham, 2014;8637:438-48.
- Gates DH, Walters LS, Cowley J, et al. Range of motion requirements for upper-limb activities of daily living. Am J Occup Ther 2016;70:7001350010p1-7001350010p10.
- Gajdosik RL, Bohannon RW. Clinical measurement of range of motion. Review of goniometry emphasizing reliability and validity. Phys Ther 1987;67:1867-72. [Crossref] [PubMed]
- de Winter AF, Heemskerk MA, Terwee CB, et al. Inter-observer reproducibility of measurements of range of motion in patients with shoulder pain using a digital inclinometer. BMC Musculoskelet Disord 2004;5:18. [Crossref] [PubMed]
- Khadilkar L, MacDermid JC, Sinden KE, et al. An analysis of functional shoulder movements during task performance using Dartfish movement analysis software. Int J Shoulder Surg 2014;8:1-9. [Crossref] [PubMed]
- Terven JR, Córdova-Esparza DM. Kin2. A Kinect 2 toolbox for MATLAB. Science of Computer Programming 2016;130:97-106. [Crossref]
- Bonnechère B, Jansen BMP, Salvia P, et al. What are the current limits of the Kinect sensor? In: Proceedings International Conference on Disability, Virtual Reality, and Associated Technologies, Laval, France, 2012:287-94.
- Sin H, Lee G. Additional virtual reality training using Xbox Kinect in stroke survivors with hemiplegia. Am J Phys Med Rehabil 2013;92:871-80. [Crossref] [PubMed]
- Kurillo G, Han JJ, Obdržálek S, et al. Upper extremity reachable workspace evaluation with Kinect. Stud Health Technol Inform 2013;184:247-53. [PubMed]
- Kurillo G, Chen A, Bajcsy R, et al. Evaluation of upper extremity reachable workspace using Kinect camera. Technol Health Care 2013;21:641-56. [Crossref] [PubMed]
- Kitsunezaki N, Adachi E, Masuda T, et al. KINECT applications for the physical rehabilitation. In: 2013 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Gatineau, Canada, 2013:294-9.
- Bonnechère B, Jansen B, Salvia P, et al. Validity and reliability of the Kinect within functional assessment activities: Comparison with standard stereophotogrammetry. Gait Posture 2014;39:593-8. [Crossref] [PubMed]
- Pfister A, West AM, Bronner S, et al. Comparative abilities of Microsoft Kinect and Vicon 3D motion capture for gait analysis. J Med Eng Technol 2014;38:274-80. [Crossref] [PubMed]
- Choppin S, Lane B, Wheat J. The accuracy of the Microsoft Kinect in joint angle measurement. Sports Technology 2014;7:98-105. [Crossref]
- Lee SH, Yoon C, Chung SG, et al. Measurement of shoulder range of motion in patients with adhesive capsulitis using a Kinect. PLoS One 2015;10:e0129398. [Crossref] [PubMed]
- Fern'ndez-Baena A, Susín A, Lligadas X. Biomechanical validation of upper-body and lower-body joint movements of Kinect motion capture data for rehabilitation treatments. In: 2012 Fourth International Conference on Intelligent Networking and Collaborative Systems, Bucharest, Romania, 2012:656-61.
- Hawi N, Liodakis E, Musolli D, et al. Range of motion assessment of the shoulder and elbow joints using a motion sensing input device: A pilot study. Technol Health Care 2014;22:289-95. [Crossref] [PubMed]
- Huber ME. Validity and reliability of Kinect skeleton for measuring shoulder joint angles: A feasibility study. Physiotherapy 2015;101:389-93. [Crossref] [PubMed]
- Knippenberg E, Verbrugghe J, Lamers I, et al. Markerless motion capture systems as training device in neurological rehabilitation: A systematic review of their use, application, target population and efficacy. J Neuroeng Rehabil 2017;14:61. [Crossref] [PubMed]
- Cuesta-Vargas AI, Galán-Mercant A, Williams JM. The use of inertial sensors system for human motion analysis. Phys Ther Rev 2010;15:462-73. [Crossref] [PubMed]
- El-Gohary M, McNames J. Shoulder and elbow joint angle tracking with inertial sensors. IEEE Trans Biomed Eng 2012;59:2635-41. [Crossref] [PubMed]
- Bachmann ER, Duman I, Usta UY, et al. Orientation tracking for humans and robots using inertial sensors. In: Proceedings IEEE International Symposium on Computational Intelligence in Robotics and Automation. CIRA'99 (Cat. No.99EX375), Monterey, CA, USA, 1999:187-94.
- Madgwick SOH, Harrison AJL, Vaidyanathan R. Estimation of IMU and MARG orientation using a gradient descent algorithm. In: 2011 IEEE International Conference on Rehabilitation Robotics, Zurich, Switzerland, 2011:1-7.
- Jonsdottir J, Bertoni R, Lawo M, et al. Serious games for arm rehabilitation of persons with multiple sclerosis: A randomized controlled pilot study. Mult Scler Relat Disord 2018;19:25-9. [Crossref] [PubMed]
- Caggianese G, Cuomo S, Esposito M, et al. Serious games and in-cloud data analytics for the virtualization and personalization of rehabilitation treatments. IEEE Transactions on Industrial Informatics 2019;15:517-26. [Crossref]
- RajKumar A, Vulpi F, Bethi SR, et al. Wearable inertial sensors for range of motion assessment. IEEE Sensors Journal 2020;20:3777-87. [Crossref] [PubMed]
- GmbH BS. BNO055 Intelligent 9-axis Absolute Orientation Sensor [Internet]. 2016. Available online: https://cdn-learn.adafruit.com/assets/assets/000/036/832/original/BST_BNO055_DS000_14.pd
- Bethi SR, RajKumar A, Vulpi F, et al. Wearable inertial sensors for exergames and rehabilitation. In: IEEE Engineering in Medicine and Biology Conference. 2020. [In press].
- Spong M, Hutchinson S, Vidyasagar M. Robot Modeling and Control. New York: Wiley, 2006:1-478.
- Chen X. Human Motion Analysis with Wearable Inertial Sensors. PhD Dissertation. University of Tennessee, Knoxville; 2013.
- Wu G, van der Helm FCT. ISB recommendation on definitions of joint coordinate systems of various joints for the reporting of human joint motion—Part II: shoulder, elbow, wrist and hand. J Biomech 2005;38:981-92. [Crossref] [PubMed]
- An KN, Morrey BF, Chao EY. Carrying angle of the human elbow joint. J Orthop Res 1984;1:369-78. [Crossref] [PubMed]
- Paraskevas G, Papadopoulos A, Papaziogas B, et al. Study of the carrying angle of the human elbow joint in full extension: A morphometric analysis. Surg Radiol Anat 2004;26:19-23. [Crossref] [PubMed]
- Sakoe H, Chiba S. Dynamic programming algorithm optimization for spoken word recognition. In: IEEE Transactions on Acoustics, Speech, and Signal Processing, 1978;2643-9.
- Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. International Journal of Nursing Studies 2010;47:931-6. [Crossref]
- Kimber AC. Exploratory data analysis for possibly censored data from skewed distributions. Journal of the Royal Statistical Society. Series C 1990;39:21-30. [Crossref]
- McGraw KO, Wong SP. Forming inferences about some intraclass correlation coefficients. Psychol Methods 1996;1:30-46. [Crossref]
- Cronbach LJ. Coefficient alpha and the internal structure of tests. Psychometrika 1951;16:297-334. [Crossref]
- Wessa P. Cronbach Alpha (v1.0.5) Free Statistics Software (v1.2.1) [Internet]. 2017. Available online: https://www.wessa.net/rwasp_cronbach.wasp/
- Brooke J. SUS: A “quick and dirty” usability scale. In: Jordan PW, Thomas B, Weerdmeester BA,et al. editors. Usability Evaluation in Industry. London: Taylor and Francis, 1996:189-94.
- Raj Kumar A, Bilaloglu S, Raghavan P, et al. Grasp rehabilitator: A mechatronic approach. In: Proceedings of the Design of Medical Devices Conference, 2019:V001T03A007.
- Feinberg C, Shaw M, Palmeri M, et al. Remotely supervised transcranial direct current stimulation (RS-tDCS) paired with a hand exercise program to improve manual dexterity in progressive multiple sclerosis: A randomized sham controlled trial. Neurology 2019;92:P5.6-009.
- RajKumar A, Arora C, Katz B, et al. Wearable smart glasses for assessment of eye-contact behavior in children with autism. In: Proceedings of the Design of Medical Devices Conference, 2019:V001T09A006.
Cite this article as: Rajkumar A, Vulpi F, Bethi SR, Raghavan P, Kapila V. Usability study of wearable inertial sensors for exergames (WISE) for movement assessment and exercise. mHealth 2021;7:4.